Division Algebra And Supersymmetry
SPIN GROUP Definition 21. Let x v1 v m then xˆ mv1 v.
In d dimensions the size of spinors is approximately 2 d2 or 2 d 12.
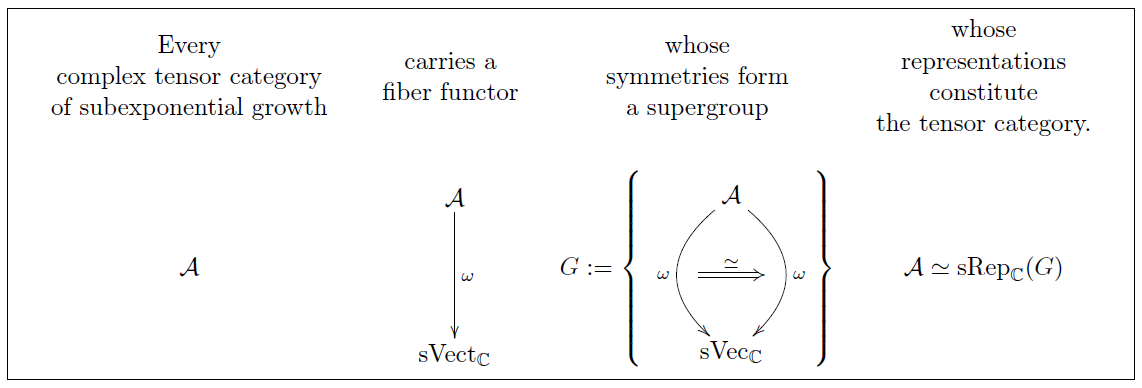
Division algebra and supersymmetry. Supersymmetry is deeply related to division algebras. The above noted associations of complex numbers and quaternions with supersymmetry can now be seen to form the following pattern. Division algebras are equivalent to objects called trialities each can be constructed from the other and the correspondence with Yang-Mills is achieved by showing that the condition for supersymmetry is equivalent to the gamma matrices decomposing to give a.
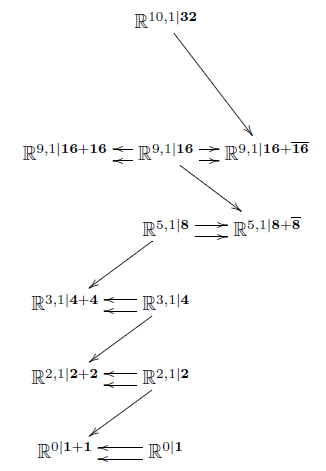
Starting from the four normed division algebras - the real numbers complex numbers quaternions and octonions - a systematic procedure gives a 3-cocycle on the Poincare Lie superalgebra in dimensions 3 4 6 and 10. They have dimensions k 1 2 4 and 8. We define the following operations on Clifford algebras 1 Reflection automorphism.
Supersymmetry is deeply related to division algebras. Let Cl V Q be the multiplicative group of units in ClV Q. Nonabelian Yang-Mills fields minimally coupled to massless spinors are supersymmetric if and only if the dimension of spacetime is 3 4 6 or 10.
LECTURES ON GEOMETRY OF SUPERSYMMETRY 5 2. Supersymmetry is deeply related to division algebras. When W 567 mod 8 so the auxiliary spaces are symplectic we instead use N.
Geometry of physics supersymmetry the section Real spin representations via Real alternative division algebra. There is a deep relation between supersymmetry and the four normed division algebras. The same is true for the Green-Schwarz superstring.
Supersymmetry and Division Algebras Normed Division Algebras Let K be a normed division algebra of dimension n. We begin with discussing the mathematical. SpinV of course is the component of PinV which lies in the even part of the Clifford algebra.
This is visible in the. And supersymmetry in quantum field theory and string theory. Even better in the octonionic case that is 11-dimensional spacetime these 2-branes are closely related to 11-dimensional supergravity.
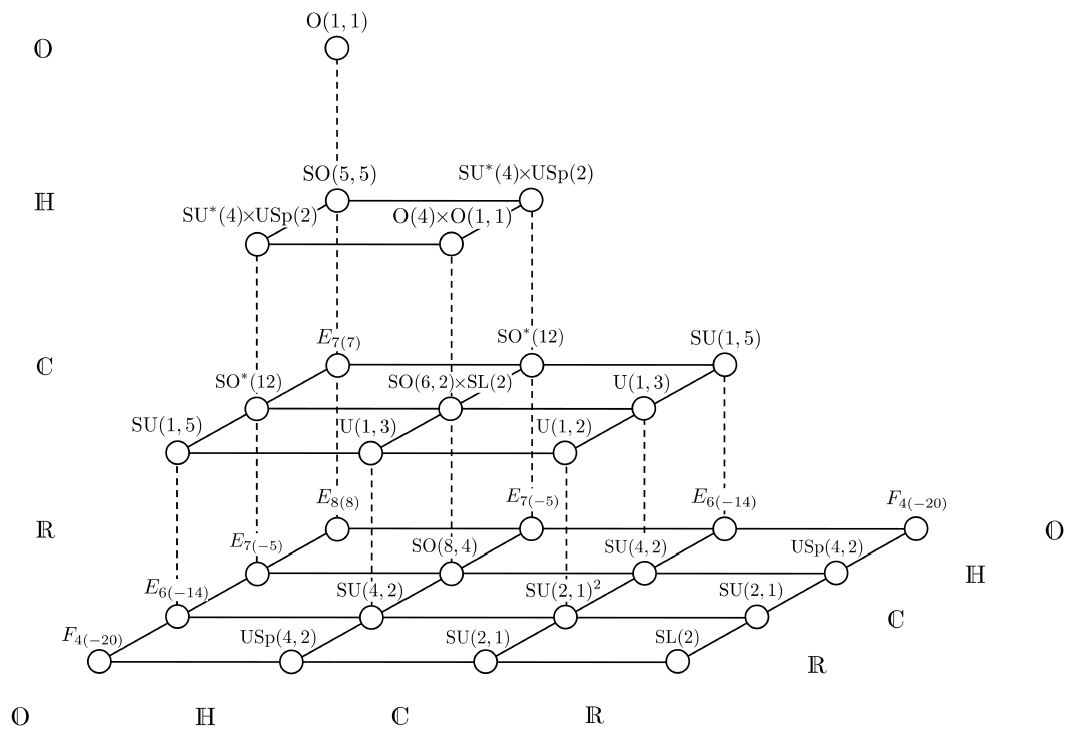
The material is supplemented with material from Quantum Theory of Fields Vol III by Weinberg Modern Supersymmetry by John Ternin as well as a few of of my own additions. Supergravity theories seen as tensor products of super ang-MillsY theories are described as tensor products of division algebras leading to the identi cation of a magic square of supergrav-ity theories with their U-duality groups as the magic square entries. It is possible to have supersymmetry in dimensions other than four.
And truncation of supersymmetry are also described here by the four division algebras. The same is true for the Green-Schwarz superstring. 13 Notice that the transverse dimension D - 2 equals the dimension of the associated division algebra.
I The classical super-2-brane makes sense only in. The structure of the normed division algebras also governs the existence of the brane scan and the. There are exceptions however.
Then I K has a conjugation a linear operator satisfying x x xy yx. Division Algebras and Supersymmetry According to Chapter 20 of Fulton and Harriss Representation Theory PinV is the set of x in CliffV such that x x 1 and x V x subseteq V. Nonabelian Yang-Mills fields minimally coupled to massless spinors are supersymmetric if and only if the dimension of spacetime is 3 4 6 or 10.
SUPERSYMMETRY LECTURE NOTES This is a set of lecture notes based primarily on a course given by Fernando Quevedo. The N 2 YM theory can also be written in a maximum of six dimensions. For example nonabelian YangMills fields minimally coupled to massless spinors are supersymmetric if and only if.
Rex x x 2 Imx x x 2. Lie n-algebras supersymmetry and division algebras Introduction This research began as a puzzle. I This allows us to define real and imaginary parts in the same way as for the complex numbers.
Holds in spacetimes of dimensions three higherthan those of the division algebras. We will introduce the classification of supersymmetry algebras using the division algebra perspective of Baez and Huerta BH10 which will be useful for the classification of super Yang-Mills. I The classical superstring makes sense only in dimensions k 2 3 4 6 and 10.
Let x v1 v m then xt v v1. So you refer to things like the 3-dimensional N 2 supersymmetry algebra. And this rule is why there exist supersymmetric 2-branes in these dimensions.
Mathbb K one of the normed division algebras see at spin group The exceptional isomorphisms. Supersymmetry in alternate numbers of dimensions. A related procedure gives a 4-cocycle on the Poincare Lie superalgebra in dimensions 4 5 7 and 11.
Because the properties of spinors change drastically between different dimensions each dimension has its characteristic. That is dimensions 4 5 7 and 11. The real numbers R the complex numbers C the quaternions H and the octonions O.
I The only normed division algebras are R C H and O. Its traditional to indicate a particular supersymmetry algebra using the dimension N or dimen-sions N N of the auxiliary spaces W or W W.

Strings Supersymmetry And The Octonions That Rule The Universe
Geometry Of Physics Supersymmetry In Nlab
Https Www Imperial Ac Uk Media Imperial College Research Centres And Groups Theoretical Physics Msc Dissertations 2013 Amel Durakovic Dissertation Pdf
From The Superpoint To T Folds In Schreiber
Geometry Of Physics Supersymmetry In Nlab
Division Algebras And Supersymmetry Iii The N Category Cafe
Geometry Of Physics Supersymmetry In Nlab
Division Algebras And Supersymmetry Ii The N Category Cafe
Geometry Of Physics Supersymmetry In Nlab
Division Algebras And Supersymmetry Iii The N Category Cafe
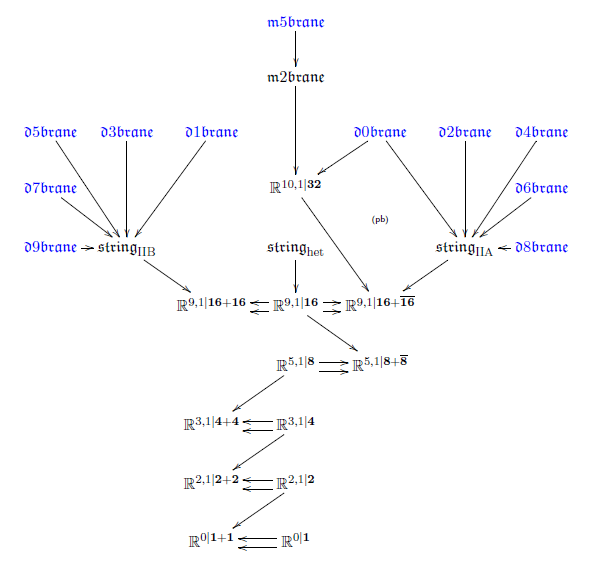
Geometry Of Physics Fundamental Super P Branes In Nlab
Https Arxiv Org Pdf 1603 09063
Normed Division Algebra In Nlab
Http Cbpfindex Cbpf Br Publication Pdfs Nf01301 2011 05 05 09 41 39 Pdf
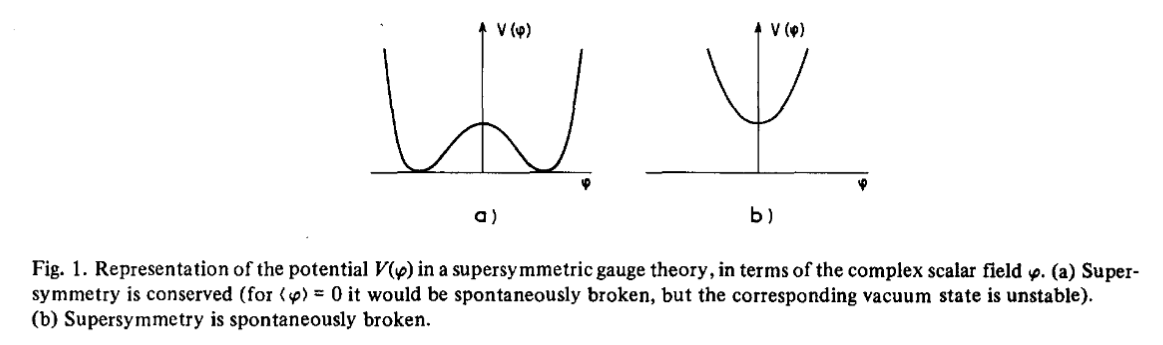
Supersymmetry Breaking In Nlab